Two proportion test is a hypothesis test that is used to determine whether the difference between two proportions is significant. This test figures out if the results are repeatable or valid. The two proportions test take a look at uses an ordinary approximation through default for calculating the speculation take a look at and self-assurance interval. The regular approximation can be used to estimate the distinction between binomial random variables which provided the model sizes are big, and size are not too near zero% or one hundred%. Similarly, while you state a test dissimilarity of 0 in the options of the sub-dialogue container, Minitab did Fisher's precise cheque, that's exact for the entire sample proportions and sizes. Fisher's genuine cheque is based on the distribution of hypergeometrics. The regular estimate may be imprecise for small numbers of activities or nonevents. If the wide variety of activities or nonevents in either pattern is fewer than five, Minitab shows a word. Fisher's genuine cheque is correct for all sample proportions and sizes. Decide whether the size of corporations fluctuates. Calculate a number values this is probably to consist of the distinction among the populace proportions. For instance, suppose you desired to understand whether or not the proportion of purchasers who go back a survey may be expanded with the aid of presenting an incentive inclusive of a product pattern.

Pooled two sample Z test of proportions formula

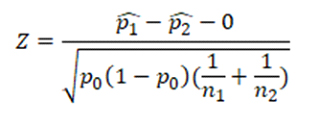
Un-pooled two sample Z test of proportions formula

For researchers from different backgrounds, it is important to have an understanding of SPSS properly. Our expertise provides you with SPSS help and is tailored with you throughout to perform your qualitative analysis, we at SPSS tutor are available to assist you–regardless of your specific research design.